Answer:
The bird is approximately 9 ft high up in the tree
Step-by-step explanation:
The required diagram is shown in the attached image
Note that the tree, the cat and the ground form a right-angled triangle
Therefore, we can apply special trigonometric functions
These functions are as follows:
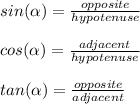
Now, taking a look at our diagram, we can note the following:
α = 25°
The opposite side is the required height (x)
The adjacent side is the distance between the cat and the tree = 20 ft
Therefore, we can use the tan function
This is done as follows:
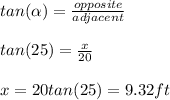 which is 9 ft approximated to the nearest ft
which is 9 ft approximated to the nearest ft
Hope this helps :)