Question

Consider triangle PQR. What is the length of side QR?

A. 8 units
B. 8/3 units
C. 16 units
D. 16/3 units

Answer 1

The length of side QR is 16 units.

Option C is correct.

Explanation:

Given a right angled triangle QPR in which length of sides are

`PQ=8\sqrt3 units`

`PR=8 units`

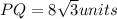
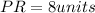
we have to find the length of side QR

As QPR is right angled triangle therefore we apply Pythagoras theorem

`(hypotenuse)^2=(Base)^2+(Perpendicular)^2`

`QR^2=PQ^2+PR^2`

`QR^2=(8\sqrt3)^2+8^2`

`QR^2=192+64=256`

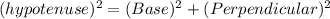
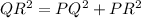
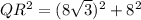
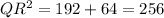
Take square root on both sides

`QR=16 units`

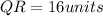
Hence, the length of side QR is 16 units.

Option C is correct.

Answer 2

C) 16

EXPLANATION

Using the Pythagoras Theorem, we obtain:

QR² =PR²+ PQ²

From the diagram,

`PQ = 8 √(3)`

`PR=8`

We substitute into the formula to get;

`|QR| ^(2) = {8}^(2) + {(8 √(3) )}^(2)`

`|QR| ^(2) = 64+ 192`

`|QR| ^(2) = 256`

Take square root

`|QR| = √(256)`

`|QR| = 16`