See the attached picture.
- Create an equation for the volume of the box, find the zeroes, and sketch the graph of the function.
The resulting box has a volume
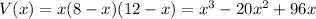
because the volume of a box is the product of its width
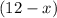 , length
, length
 , and height
, and height
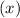 .
.
You know right away from the factored form of
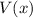 that the zeroes are
that the zeroes are
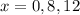 . (zero product property)
. (zero product property)
- sketch the graph of the function
Easy to plot by hand. You know the zeroes, and you can check the sign of
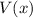 for any values of
for any values of
 between these zeros to get an idea of what the graph of
between these zeros to get an idea of what the graph of
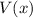 looks like. See the second attached picture.
looks like. See the second attached picture.
Here's what I mean by "check the sign" in case you don't follow. We know
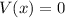 when
when
 and
and
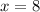 . So we pick some value of
. So we pick some value of
 between them, say
between them, say
 , and find that
, and find that
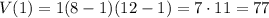
which is positive, so
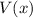 will be positive for any other
will be positive for any other
 between 0 and 8. Similarly we would find that
between 0 and 8. Similarly we would find that
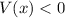 for
for
 between 8 and 12, and so on.
between 8 and 12, and so on.
- What is the size of the cutout he needs to make so that he can fit the most marbles in the box?
It's impossible to answer this without knowing the volume of each marble...
- If Thomas wants a volume of 12 cubic inches, what size does the cutout need to be?
Thomas wants
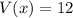 , so you solve
, so you solve
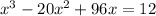
While this is possible to do by hand, the procedure is tedious (look up "solving the cubic equation"). With a calculator, you'd find three approximate solutions
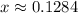


but you throw out the third solution because, realistically, the cutout length can't be greater than either of the sheet's dimensions.
- What would be the dimensions of this box?
The box's dimensions are (
 in) x (
in) x (
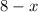 in) x (
in) x (
 in).
in).
If
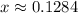 , then
, then
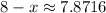 and
and
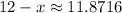 .
.
If
 , then
, then
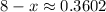 and
and
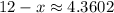 .
.