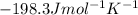Question

Calculate the entropy change for the reaction: N2(g) + 3H2(g) -> 2NH3(g)

Entropy data:
NH3 = 192.5 J/mol K
H2 = 130.6 J/mol K
N2 = 191.5 J/mol K

Answer 1

Answer: The
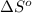`\Delta S^o` of the reaction is
`-198.3Jmol^(-1)K^(-1)`

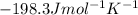
Step-by-step explanation:

Entropy change of the reaction is defined as the difference between the total entropy change of the products and the total entropy change of the reactants.

Mathematically,

`\Delta S_(rxn)=\sum [n* \Delta S^o_(products)]-\sum [n* \Delta S^o_(reactants)]`

For the given chemical equation:

`N_2(g)+3H_2(g)\rightarrow 2NH_3(g)`

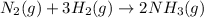
We are given:

`\Delta S^o_(NH_3)=192.5Jmol^(-1)K^(-1)\\\Delta S^o_(H_2)=130.6Jmol^(-1)K^(-1)\\\Delta S^o_(N_2)=191.5Jmol^(-1)K^(-1)`

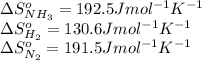
Putting values in above equation, we get:

`\Delta S^o_(rxn)=[(2* \Delta S^o_(NH_3))]-[(1* \Delta S^o_(N_2))+(3* \Delta S^o_(H_2))]`

`\Delta S^o=[(2* 192.5)]-[(1* 191.5)+(3* 130.6)]=-198.3Jmol^(-1)K^(-1)`

Hence, the
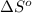`\Delta S^o` of the reaction is
`-198.3Jmol^(-1)K^(-1)`

Answer 2

ΔS⁰ = -198.3 J/K

Step-by-step explanation:

N₂(g) + 3H₂(g) → 2NH₃(g)

S⁰: N₂(g) = 1mole(191.5J/mole·K) = 191.5J/K

S⁰: 3H₂(g) = 3moles(130.6J/mole·K) = 391.8J/K

S⁰: 2NH₃(g) = 2moles(192.5J/mole·K) = 385J/K

ΔS⁰ = ∑n·S⁰(Products) - ∑n·S⁰(Reactants

=[385J/K] - [191.5J/K + 391.8J/K]

= (385 - 191.5 - 391.8)J/K

= -198.3J/K