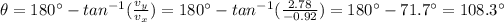Question

ANSWER PLEASE LORD ANSWER

Answer 1

< 2.11, 4.53 >, < -3.03, -1.75 >, <2.93 cos 108.26, 2.93 sin 108.26 >

Answer 2

< 2.11, 4.53 >, < -3.03, -1.75 >, <2.93 cos 108.26, 2.93 sin 108.26 >

Explanation:

First, let's decompose Bruce's velocity along the x- and y- direction. Bruce is moving 5 m/s at 25 degrees east of north, so its angle with respect to the positive x-direction is actually 90 - 25 = 65 degrees. So its components are

`b_x = (5 m/s) cos 65^(\circ) =2.11 m/s\\b_y = (5 m/s) sin 65^(\circ) =4.53 m/s`

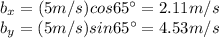
So, Bruce's vector is

< 2.11, 4.53 >

The current is moving 3.5 m/s at an angle 60 degrees west of south, which means an overall angle of 210 degrees, measured counterclockwise from the positive x-axis. So, the components of the current's velocity are

`c_x = (3.5 m/s) cos 210^(\circ)=-3.03 m/s\\c_y = (3.5 m/s) sin 210^(\circ)=-1.75 m/s`

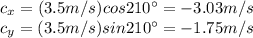
So, the current's vector is

< -3.03, -1.75 >

Finally, we can add the components of the two vectors to find Bruce's actual velocity:

`v_x = b_x + c_x = 2.11 + (-3.03)=-0.92 m/s\\v_y = b_y + c_y = 4.53+(-1.75)=2.78 m/s`

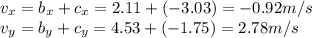
So, Bruce's actual velocity is

< -0.92, 2.78 >

The magnitude is

`v=√((-0.92)^2+(2.78)^2)=2.93 m/s`

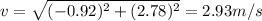
And the direction is

`\theta=180^(\circ) - tan^(-1) ((v_y)/(v_x))=180^(\circ) - tan^(-1)((2.78)/(-0.92))=180^(\circ)-71.7^(\circ)=108.3^(\circ)`