Question

I need to find the measure of each angle indicated please help

Answer 1

We shall use the mnemonics SOH-CAH-TOA to find the missing angles.

SOH- means sine ratio is
`(Opposite)/(Hypotenuse)`

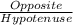
CAH- means cosine ratio is
`(Adjacent)/(Hypotenuse)`

TOA- means tangent ratio is
`(Opposite)/(Adjacent)`

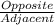
11) From the given right-angle triangle,the side length adjacent to
`\theta` is 11 units.

The opposite side is 8 units.

We use the tangent ratio to obtain:

`\tan \theta=(8)/(11)`

`\theta=\tan ^(-1)((8)/(11))`

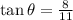
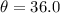`\theta=36.0\degree` to the nearest tenth.

12) From the given right-angle triangle,the side length adjacent to
`\theta` is 7 units.

The opposite side is 13 units.

We use the tangent ratio to obtain:

`\tan \theta=(13)/(7)`

`\theta=\tan ^(-1)((13)/(7))`

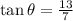
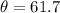`\theta=61.7\degree` to the nearest tenth.

13) From the given right-angle triangle,the side length adjacent to
`\theta` is 8 units.

The opposite side is 11 units.

We use the tangent ratio to obtain:

`\tan \theta=(11)/(8)`

`\theta=\tan ^(-1)((11)/(8))`

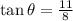
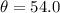`\theta=54.0\degree` to the nearest tenth.

14. This time we were given the hypotenuse to be 9.7 units and the opposite side of the right-angle triangle is 7 units.

We use the sine ratio to obtain:

`\sin \theta=(7)/(9.7)`

`\implies \sin \theta=(70)/(97)`

`\implies \sin \theta=(70)/(97)`

`\implies \theta=\sin^(-1)((70)/(97))`

`\implies \theta=46.2\degree`

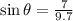
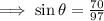
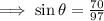
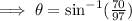
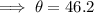
15. For question 15; we the hypotenuse to be 7 units and the adjacent side is 4 units.

We use the cosine ratio to get;

`\cos \theta=(4)/(7)`

`\implies \theta=\cos^(-1)((4)/(7))`

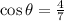
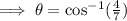
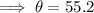`\implies \theta=55.2\degree` to the nearest tenth.

16) From the given right-angle triangle,the side length adjacent to
`\theta` is 13 units.

The opposite side is 12 units.

We use the tangent ratio to obtain:

`\tan \theta=(12)/(13)`

`\theta=\tan ^(-1)((12)/(13))`

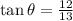
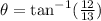
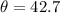`\theta=42.7\degree` to the nearest tenth.