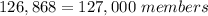Answer:
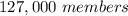
Explanation:
In this problem we have an exponential function of the form
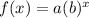
where
a is the initial value
b is the base
The base is equal to
b=1+r
r is the average rate
In this problem we have
a=23,000 members
r=5%=5/100=0.05
b=1+0.05=1.05
substitute
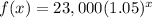
x ----> is the number of years since 1985
How many members will there be in 2020?
x=2020-1985=35 years
substitute in the function
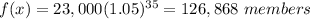
Round to the nearest thousand