Answer:
Explanation:
This is a third degree polynomial because we are given three roots to multiply together to get it. Even though we only see "2 + i" the conjugate rule tells us that 2 - i MUST also be a root. Thus, the 3 roots are x = -4, x = 2 + i, x = 2 - i.
Setting those up as factors looks like this (keep in mind that the standard form for the imaginary unit in factor form is ALWAYS "x -"):
If x = -4, then the factor is (x + 4)
If x = 2 + i, then the factor is (x - (2 + i)) which simplifies to (x - 2 - i)
If x = 2 - i, then the factor is (x - (2 - i)) which simplifies to (x - 2 + i)
Now we can FOIL all three of those together, starting with the 2 imaginary factors first (it's just easier that way!):
(x - 2 - i)(x - 2 + i) =

Combining like terms and canceling out the things that cancel out leaves us with:
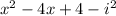
Remembr that
 , so we can rewrite that as
, so we can rewrite that as
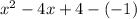 and
and
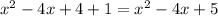
That's the product of the 2 imaginary factors. Now we need to FOIL in the real factor:
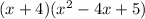
That product is
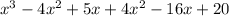
which simplifies down to
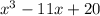
And there you go!