Question

The table below shows the probability distribution of the number of credit cards people own. What is the probability (as a percentage) that a person will have at least three credit cards

Answer 1

28%

Explanation:

From the table, the probability that the person will have

• 0 credit cards - 0.16;
• 1 credit card - 0.12;
• 2 credit cards - X;
• 3 credit cards - Y;
• 4 credit cards - 0.72

The sum of all probabilities must equal to 1, so

`0.16+0.12+X+Y+0.72=1\\ \\X+Y=1-0.16-0.12-0.72\\ \\X+Y=0`

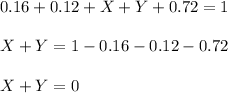
The probability that a person will have at most 3 credit cards is

`Pr(\text{at most 3 credit cards})=Pr(\text{0 credit cards})+Pr(\text{1 credit card})+Pr(\text{2 credit cards})+Pr(\text{ 3 credit cards})=0.16+0.12+X+Y=0.28+0=0.28`

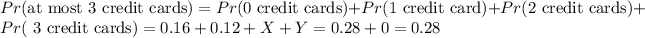
and as a percentage 28%