Question

Describe how the graph of g(x) is related to the parent function f(x). f(x) = 4^x g(x) = 4^x – 2

Answer 1

The graph of f(x) is shifted to right by 2 units to get graph of g(x).

Explanation:

We have been given two functions
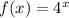`f(x)=4^x` and
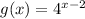`g(x)=4^(x-2)`. We are asked to find the graph of g(x) is related to the parent function f(x).

Let us recall transformation rules.

`f(x)\rightarrow f(x-a)=\text{Graph shifted to right by a units}`

`f(x)\rightarrow f(x+a)=\text{Graph shifted to left by a units}`

`f(x)\rightarrow f(x)-a=\text{Graph shifted downwards by a units}`

`f(x)\rightarrow f(x)+a=\text{Graph shifted upwards by a units}`

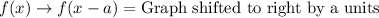
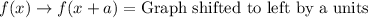
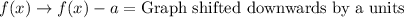
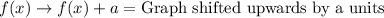
Upon comparing the graph of f(x) to g(x), we can see that
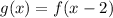`g(x)=f(x-2)`, therefore, the graph of f(x) is shifted to right by 2 units to get graph of g(x).

Answer 2

g(x) is translated down 2 units from f(x)

Explanation:

Adding -2 to the function value moves it down 2 units.