Rewriting
 in polar form makes this trivial.
in polar form makes this trivial.
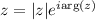
We have
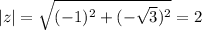
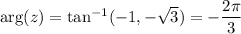
(not to be confused with the standard inverse tangent function
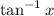 . Here
. Here
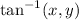 is the inverse tangent function that takes into account position in the coordinate plane; look up "atan2" for more information)
is the inverse tangent function that takes into account position in the coordinate plane; look up "atan2" for more information)
So we have
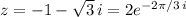
Then
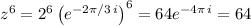
so that
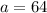 and
and
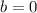 .
.