Question

Scoring scheme: 3-3-2-1 for many reactions near room temperature, the rate and the rate constant approximately double for a 10 °c rise in temperature. what is the value of activation energy in kj/mol for such a reaction

Answer 1

\boxed{\text{52.9 kJ/mol}}

Step-by-step explanation:

To solve this problem, we must use the Arrhenius equation:

`\ln (k_(2))/(k_(1)) = (E_(a))/(R)\left((1)/(T_(2)) - (1)/(T_(1))\right)`

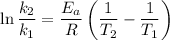
The activation energy depends on the starting temperature, so, let's assume that

T₁ = 25 °C = 298.15 K

T₂ = 35 °C = 308.15 K

k₂/k₁ = 2

This gives

`\ln (k_(2))/(k_(1)) = (E_(a))/(R)\left((1)/(T_(2)) - (1)/(T_(1))\right)\\\\\ln (2)/(1) = (E_(a))/(8.314)\left((1)/(308.15) - (1)/(298.15)\right)\\\\\ln 2 = (E_(a))/(8.314)\left(3.3540 * 10^(-3) - 3.2452* 10^(-3)\right)\\\\8.314 \ln 2 = E_(a)\left(1.088 * 10^(-4)\right)\\\\E_(a) = (8.314 \ln 2)/(1.088 * 10^(-4))\\\\E_(a) = 5.29 * 10^(4)\text{ J/mol}\\\\E_(a) = \boxed{\textbf{52.9 kJ/mol}}`