Answer: odd
Explanation:
A function is even if for any input value x and -x there is the same output value y. In other words, a function is even if:
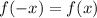
A function is odd if it is true that:
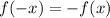
Then we must test if
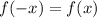 for the function:
for the function:
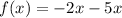
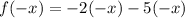
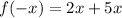
So
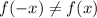
The function is not even
Now we must test if
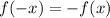 for the function.
for the function.
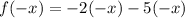
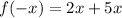
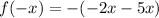 and
and
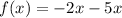
So
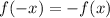
Finally the function is odd