For this case we have to find the inverse of a function, follow the steps below:
- We exchange the variables.
- Finally we change y by
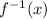
Then, it is observed that of option 3:
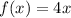
Replace
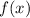 with y:
with y:
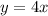
We exchange the variables:

We solve for "y":
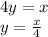
Finally we change y by
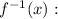
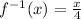
Answer:
The correct option is C