Question

Factorize completely -3c²-4cb+4b²​

Answer 1

I'll focus on part (b) only.

Answers:

• Part (i): The factorization is (2b-3c)(2b+c)
• Part (ii): The expression evaluates to -11

======================================================

Step-by-step explanation:

Replace the variable b with the commonly used variable x and c with some other constant, let's say the letter m. These replacements will become apparent when we use the quadratic formula shortly later on.

After the replacements are made, we have -3c²-4cb+4b²​ turn into -3m²-4mx+4x²​

This is the same as 4x²​-4mx-3m²

Compare this to the format of ax²​+bx+c

We can see that

• a = 4
• b = -4m
• c = -3m²

Once again, m is constant.

Let's compute the discriminant.

`d = b^2 - 4ac\\\\d = (-4m)^2-4(4)(-3m^2)\\\\d = 16m^2+48m^2\\\\d = 64m^2\\\\`

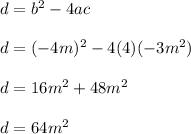
This discriminant is under the square root as part of the quadratic formula.

So 4x²​-4mx-3m² would have roots of...

`x = (-b\pm√(b^2-4ac))/(2a)\\\\x = (-b\pm√(d))/(2a)\\\\x = (-(-4m)\pm√(64m^2))/(2(4))\\\\x = (4m\pm√((8m)^2))/(8)\\\\x = (4m\pm 8m)/(8)\\\\x = (4(m\pm 2m))/(4*2)\\\\x = (m\pm 2m)/(2)\\\\x = (m+ 2m)/(2) \ \text{ or } \ x = (m-2m)/(2)\\\\x = (3m)/(2) \ \text{ or } \ x = (-m)/(2)\\\\`

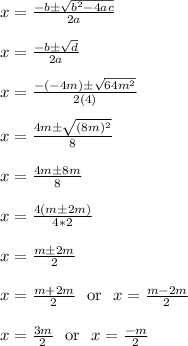
The whole time, the term "m" is treated as a constant. It is fixed to some unchanging number.

So why did we go through all that trouble to use the quadratic formula in the first place? It turns out that this formula is helpful to factoring quadratics. Recall that the roots of a polynomial tie very closely to its factorization.

For example, x²-4 factors to (x-2)(x+2) to have roots of x = 2 or x = -2. You could use the quadratic formula to solve x²-4 = 0 or x²+0x-4 = 0 and you should get x = 2 or x = -2 as the two solutions.

Anyways, back to the problem at hand.

Let's use the first root we found to form one of the factors needed.

The idea is to do a bit of algebra to get everything to one side. If fractions are present, then multiply both sides by the LCD to clear them out. We need to have 0 isolated on its own side.

`x = (3m)/(2) \\\\ 2x = 3m\\\\ 2x-3m = 0`

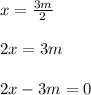
So (2x-3m) is one factor

Through similar steps, you would find that the root
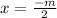`x = (-m)/(2)` yields the factor of (2x+m)

Therefore, the factors are (2x-3m) and (2x+m)

------------------------------------

In summary so far, 4x²​-4mx-3m² factors to (2x-3m)(2x+m)

From here we replace x with b and replace m with c, so that we return back to the original variables used.

(2x-3m)(2x+m) becomes (2b-3c)(2b+c)

This can be confirmed using WolframAlpha. You could use the FOIL rule to expand out (2b-3c)(2b+c) and you should get 4b²​-4bc-3c²​ aka -3c²-4cb+4b²​

-------------------------------------

Those previous sections talked about part (i)

Part (ii) is where we plug in b = 4 and c = 3. In other words, we replace every copy of b with 4, and every copy of c with 3.

If you use the original expression, then,

-3c²-4cb+4b²​ = -3(3)²-4(3)(4)+4(4)²​ = -3(9)-4(12)+4(16) = -11

Or you could use the factored expression.

(2b-3c)(2b+c) = (2*4-3*3)(2*4+3) = (8-9)(8+3) = (-1)*(11) = -11

This very partially confirms that -3c²-4cb+4b² = (2b-3c)(2b+c) is indeed the case. Unfortunately you'd have to use infinitely many numeric examples to confirm the answer to part (i); however, something like the FOIL rule is far more efficient.

Answer 2

-3(3)^3 - 4(3)(4) + 4(4)^2
-3(9) - 4(12) + 4(16)
-27 - 48+ 64
-75+64
-11
The answer is-11