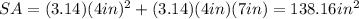Answer: 138.16 in²
Explanation:
You need to use this formula to calculate the surface area of the cone:
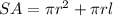
Where "r" is the radius, "h" is the height and "l" is the slant height.
To find the height you need to use the Pythagorean Theorem:
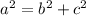
Where "a" is the hypotenuse and "b" and "c" are the legs of the triangle.
In this case:
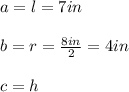
("r" is the radius and "h" is the height and "l" is the slant height.)
You need to find "h". Then, solving for "h", you get:
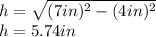
Then, substituting values into the formula, you get: