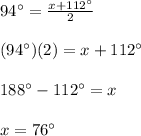Answer:

Explanation:
By definition the angle formed by the intersection of two chords inside a circle is:
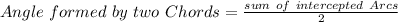
You can observe in the figure that the angle formed by the intersection of the two chords measures 94°, and the intercepteed arcs are: x° and 112°.
Therefore, you need to substitute these values into the formula and solve for "x to find its value. Then: