Question

Ther are 6 girls and 7 boys in a class. A team of 10 players is to be selected from the class. How many different combinations of players are possible

Answer 1

`13C10 =286`

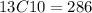
Explanation:

To solve this problem we must use the formula of combinations.

`nCr =(n!)/(r!(n-r)!)`

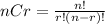
Where n is the number of players that there are and elect r of them

In this case there are
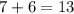`7 + 6 = 13` players and you choose 10 of them

Then we look for 13C10

`13C10 =(13!)/(10!(13-10)!)`

`13C10 =(13!)/(10!*3!)`

`13C10 =286`

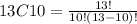
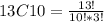
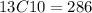
There are 286 possible combinations