Question

Let f(x) = 1/x and g(x) = x^2 + 4x. What
two numbers are not in the domain of fºg?

Answer 1

0 and -4

Explanation:

We have been given the following functions;

f(x) = 1/x

g(x) = x^2 + 4x

The first step would be to evaluate the composite function fºg.

fºg = f[g(x)]. We substitute g(x) in place of x in f(x)

fºg =
`(1)/(g(x))=(1)/(x^(2)+4x)`

This is clearly a rational function which will be defined everywhere except where the expression in the denominator will be equal to 0.

We solve for x;

`x^(2)+4x=0\\\\x(x+4)=0\\x=0\\x=-4`

Therefore, the two numbers that are not in the domain of fºg are 0 and -4

Answer 2

For this case we have the following equations:

`f (x) = \frac {1} {x}\\g (x) = x ^ 2 + 4x`

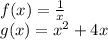
We must find (f_ {o} g) (x):

By definition of composition of functions we have to:

`(f_ {o} g) (x) = f (g (x))`

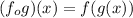
So:

`(f_ {o} g) (x) = \frac {1} {x ^ 2 + 4x}`

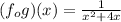
We must find the domain of
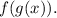`f (g (x)).` The domain will be given by the values for which the function is defined, that is, when the denominator is nonzero.

`x ^ 2 + 4x = 0\\x (x + 4) = 0`

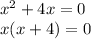
So, the roots are:

`x_ {1} = 0\\x_ {2} = - 4`

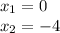
The domain is given by all real numbers except 0 and -4

Answer:

x other than 0 and -4