Answer:
There are 286 possible combinations
Explanation:
To solve this problem we must use the formula of combinations.
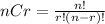
Where n is the number of players that there are and elect r of them
In this case there are 7 + 6 = 13 players and you choose 10 of them
Then we look for 13C10
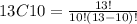
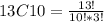

There are 286 possible combinations