ANSWER
True
Step-by-step explanation
The given trigonometric equation is:
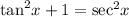
We take the LHS and simplify to arrive at the RHS.

Collect LCM on the right hand side to get;
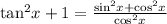
This implies that
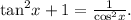
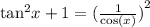
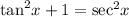
This identity has been verified .Therefore the correct answer is true.