Question

True or false: the equation tan^2x+1=sec^2x

Answer 1

True

Step-by-step explanation

The given trigonometric equation is:

`{ \tan}^(2) x + 1 = { \sec}^(2) x`

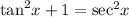
We take the LHS and simplify to arrive at the RHS.

`{ \tan}^(2) x + 1 = \frac{{ \sin}^(2) x}{{ \cos}^(2) x} + 1`

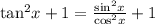
Collect LCM on the right hand side to get;

`{ \tan}^(2) x + 1 = \frac{{ \sin}^(2) x + {\cos}^(2) x}{{ \cos}^(2) x}`

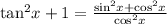
This implies that

`{ \tan}^(2) x + 1 = \frac{1}{{ \cos}^(2) x} .`

`{ \tan}^(2) x + 1 = {( (1)/( \cos(x) )) }^(2)`

`{ \tan}^(2) x + 1 = { \sec}^(2) x`

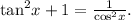
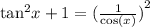
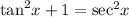
This identity has been verified .Therefore the correct answer is true.