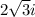2 Answers

Yash Tamakuwala · Answer 1 · 2020-10-16T18:25:25+0000

ANSWER

2 √(3) i

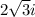
EXPLANATION

We we're given that, the real part of the complex number is 2.

Let the imaginary part be y.

Then the complex number is

z = 2 + yi

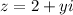
Also, we have that, the modulus is 4.

The modulus is given by the formula;

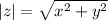
$|z| = \sqrt{ {x}^(2) + {y}^(2) }$

This implies that,

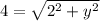
$4 = \sqrt{ {2}^(2) + {y}^(2) }$

We square both sides to obtain;

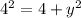
${4}^(2) = 4 + {y}^(2)$

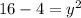
$16 - 4 = {y}^(2)$

${y}^(2) = 12$

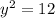
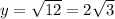
y = √(12) = 2 √(3)

Therefore the complex part is

2 √(3) i

Please log in or register to add a comment.