Answer:
Explanation:
Given that a researcher interested in Springfield citizens' shopping habits surveys a randomly selected group of 200 Walmart shoppers. 76% of those surveyed indicated that price was more important to them than where an item was produced.
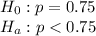
(One tailed test)
Sample proportion p = 0.76
p difference = 0.01
Std error =
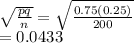
Test statistic z = p difference / std error =
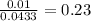
p value = 0.409
Since p >0.05 we accept null hypothesis.
There is no statistical evidence to prove that proportion >3/4 or 0.75