Answer:
Approximately
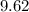 .
.
Step-by-step explanation:
![y_1 = 4.85\, \sin[(4.35\, x - 1270\, t) + 0]](https://img.qammunity.org/2022/formulas/physics/college/kd4oi2369hpye73gva55o0sbrq3hklh571.png) .
.
![y_2 = 4.85\, \sin[(4.35\, x - 1270\, t) + (-0.250)]](https://img.qammunity.org/2022/formulas/physics/college/jeye9yejswboeyt5ufjhni3sizqcmb3h3l.png) .
.
Notice that sine waves
 and
and
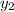 share the same frequency and wavelength. The only distinction between these two waves is the
share the same frequency and wavelength. The only distinction between these two waves is the
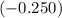 in
in
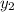 .
.
Therefore, the sum
 would still be a sine wave. The amplitude of
would still be a sine wave. The amplitude of
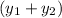 could be found without using calculus.
could be found without using calculus.
Consider the sum-of-angle identity for sine:
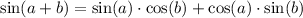 .
.
Compare the expression
 to
to
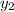 . Let
. Let
 and
and
 . Apply the sum-of-angle identity of sine to rewrite
. Apply the sum-of-angle identity of sine to rewrite
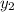 .
.
![\begin{aligned}y_2 &= 4.85\, \sin[(\underbrace{4.35\, x - 1270\, t}_(a)) + (\underbrace{-0.250}_(b))]\\ &= 4.85 \, [\sin(4.35\, x - 1270\, t)\cdot \cos(-0.250) \\ &\quad\quad\quad\; + \cos(4.35\, x - 1270\, t)\cdot \sin(-0.250)] \end{aligned}](https://img.qammunity.org/2022/formulas/physics/college/migmvndy6xkdr6r4dt2wqfyzxm18zl8468.png) .
.
Therefore, the sum
 would become:
would become:
![\begin{aligned}& y_1 + y_2\\[0.5em] &= 4.85\, [\sin(4.35\, x - 1270\, t) \\ &\quad \quad \quad\;+\sin(4.35\, x - 1270\, t)\cdot \cos(-0.250) \\ &\quad\quad\quad\; + \cos(4.35\, x - 1270\, t)\cdot \sin(-0.250)] \\[0.5em] &= 4.85\, [\sin(4.35\, x - 1270\, t)\cdot (1 + \cos(-0.250)) \\ &\quad\quad\quad\; + \cos(4.35\, x - 1270\, t)\cdot \sin(-0.250)] \end{aligned}](https://img.qammunity.org/2022/formulas/physics/college/9dameue4f00lb5hixxqyeaxpokvhgcnsqu.png) .
.
Consider: would it be possible to find
 and
and
 that satisfy the following hypothetical equation?
that satisfy the following hypothetical equation?
![\begin{aligned}& (4.85\, m)\cdot \sin((4.35\, x - 1270\, t) + c)\\&= 4.85\, [\sin(4.35\, x - 1270\, t)\cdot (1 + \cos(-0.250)) \\ &\quad\quad\quad\; + \cos(4.35\, x - 1270\, t)\cdot \sin(-0.250)] \end{aligned}](https://img.qammunity.org/2022/formulas/physics/college/k2mv5cr1j49y3igxa5tn2wumv9xk8nph4l.png) .
.
Simplify this hypothetical equation:
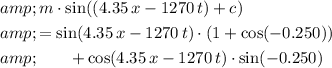 .
.
Apply the sum-of-angle identity of sine to rewrite the left-hand side:
![\begin{aligned}& m\cdot \sin((4.35\, x - 1270\, t) + c)\\[0.5em]&=m\, \sin(4.35\, x - 1270\, t)\cdot \cos(c) \\ &\quad\quad + m\, \cos(4.35\, x - 1270\, t)\cdot \sin(c) \\[0.5em] &=\sin(4.35\, x - 1270\, t)\cdot (m\, \cos(c)) \\ &\quad\quad + \cos(4.35\, x - 1270\, t)\cdot (m\, \sin(c)) \end{aligned}](https://img.qammunity.org/2022/formulas/physics/college/17z1t4g4o6xu6mgh3t5j6toeveiznxgsh6.png) .
.
Compare this expression with the right-hand side. For this hypothetical equation to hold for all real
 and
and
 , the following should be satisfied:
, the following should be satisfied:
 , and
, and
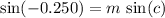 .
.
Consider the Pythagorean identity. For any real number
 :
:
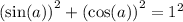 .
.
Make use of the Pythagorean identity to solve this system of equations for
 . Square both sides of both equations:
. Square both sides of both equations:
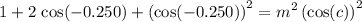 .
.
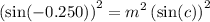 .
.
Take the sum of these two equations.
Left-hand side:
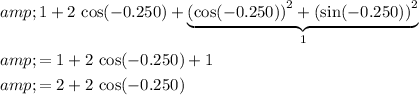 .
.
Right-hand side:
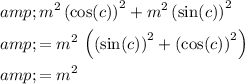 .
.
Therefore:
 .
.
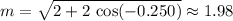 .
.
Substitute
 back to the system to find
back to the system to find
 . However, notice that the exact value of
. However, notice that the exact value of
 isn't required for finding the amplitude of
isn't required for finding the amplitude of
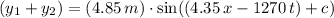 .
.
(Side note: one possible value of
 is
is
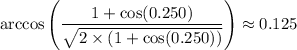 radians.)
radians.)
As long as
 is a real number, the amplitude of
is a real number, the amplitude of
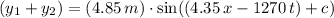 would be equal to the absolute value of
would be equal to the absolute value of
 .
.
Therefore, the amplitude of
 would be:
would be:
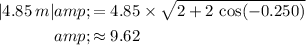 .
.