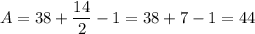Question

Question 13 (2 points)
Find the area of the composite figure. Help plz

Answer 1

44 units²

Explanation:

The Pick's theorem

Let P be a polygon in the plane whose vertices have integer coordinates. Then the area of P can be determined just by counting the lattice points on the interior and boundary of the polygon!

In fact, the area is given by

`A=i+(b)/(2)-1`

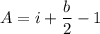
where i is the number interior lattice points, and b is the number of boundary lattice points.

Look at the picture.

i = 38

b = 14

Substitute:

`A=38+(14)/(2)-1=38+7-1=44`