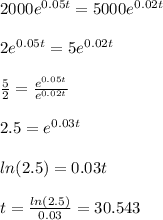Answer:
30.54 yrs
Explanation:
We have been given the following exponential growth functions;
Species A;
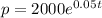
Species B;
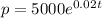
where t = 0 in 2010.
We are required to determine the number of years it will take for the populations of both species to be equal.
To do this we simply equate the two exponential functions and solve for t;