Question

Find the values of m and b that make the following function differentiable.

f(x) = {x^2, x less than or equal to 2
mx+b, x>2}
thank you so much!!

Answer 1

Both x² and mx + b are differentiable functions of x (they are both polynomials), so if f(x) is also differentiable, we need to pay special attention at x = 2 where the two pieces of f meet.

Continuity means that the limit

`\displaystyle \lim_(x\to2) f(x)`

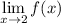
must exist.

From the left side, we have x < 2 and f(x) = x², so

`\displaystyle \lim_(x\to2^-) f(x) = \lim_(x\to2) x^2 = 4`

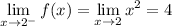
From the right, we have x > 2 and f(x) = mx + b, so

`\displaystyle \lim_(x\to2^+) f(x) = \lim_(x\to2) (mx+b) = 4m+b`

It follows that 4m + b = 4.

Differentiability means that the limit

`\displaystyle \lim_(x\to2) (f(x) - f(2))/(x - 2)`

must exist.

From the left side, we again have x < 2 and f(x) = x². Then

`\displaystyle \lim_(x\to2^-)(f(x)-f(2))/(x-2) = \lim_(x\to2) (x^2-4)/(x-2) = \lim_(x\to2) (x+2) = 4`

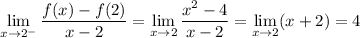
From the right side side, we have x > 2 so f(x) = mx + b. Then

`\displaystyle \lim_(x\to2^+)(f(x)-f(2))/(x-2) = \lim_(x\to2) ((mx+b)-(2m+b))/(x-2) = \lim_(x\to2) (mx-2m)/(x-2) = \lim_(x\to2)m = m`

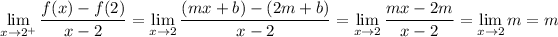
The one-sided limits must be equal, so m = 4, and from the other constraint it follows that 16 + b = 4, or b = -12.