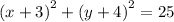Question

What is the standard equation of the circle with radius 5 and the center (-3, -4)?

Answer 1

`{(x + 3)}^(2) + {(y + 4)}^(2) = 25`

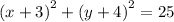
EXPLANATION

The equation of a circle with center (h,k) and radius r units is given by:

`{(x - h)}^(2) + {(y - k)}^(2) = {r}^(2)`

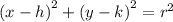
From the given information the center of the circle is (-3,-4) and the radius is r=5 units.

We substitute the known values to obtain:

`{(x - - 3)}^(2) + {(y - - 4)}^(2) = {5}^(2)`

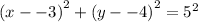
We simplify to get:

`{(x + 3)}^(2) + {(y + 4)}^(2) = 25`

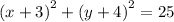
Therefore the equation of the circle in standard form is:

`{(x + 3)}^(2) + {(y + 4)}^(2) = 25`

Answer 2

(x+3)² + (y+4)²=25

Explanation:

The question is on equation of a circle

The distance formula is given by;

√(x-h)²+ (y-k)²=r

The standard equation of circle is given as ;

(x-h)²+ (y-k)²=r²

The equation of this circle with center (-3, -4) and radius 5 will be;

(x--3)² + (y--4)²=5²

(x+3)² + (y+4)²=25