Question

Can you show work for all of these and match them

Answer 1

I'll show you how to do one of the equations and one of the inequalities. All the others are done exactly in the same way: you'll only have to change the numbers, and it will be a good exercise.

Equations

Let's take the first equality as an example: we have

`|x-2|=5`

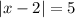
By definition, the absolute value of a number is the positive version of that number: if the number is already positive the absolute value doesn't change it; if a number is negative the absolute value changes its sign.

So, if the absolute value of a number is 5, than that number was already 5, or it was -5, and the absolute value changed it to positive 5.

So, the solutions are given by

`|x-2|=5 \iff x-2=5 \lor x-2 = -5 \iff x=7 \lor x=-3`

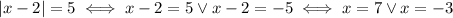
Inequalities

Again, we'll use the first one as example. We have

`|x+4|\geq 7`

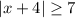
By the same logic as before, the absolute value of a number is greater than 7 if the number is already greater than 7, or if it is smaller than -7. For example, we have |-10|=10>7.

So, we have

`|x+4|\geq 7 \iff x+4 \geq 7 \lor x+4 \leq -7 \iff x \geq 3 \lor x \leq -11`

Instead, if we have an inequality with the "less than" sign, we have for example

`|x-5|\leq 8 \iff -8 \leq x-5 \leq 8 \iff -3 \leq x \leq 13`