2 Answers

Jamix · Answer 1 · 2020-02-10T09:00:38+0000

Hello!

The answer is:

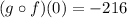
$(g\circ f)(0)=-216$

To composite functions, we need to evaluate functions in another function(s), for example:

Given f(x) and g(x), if we want to calculate f(x) composite g(x), we need to evaluate g(x) into f(x).

So, we are given the functions:

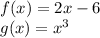
$f(x)=2x-6\\g(x)=x^(3)$

And we are asked to calculate g(x) composite f(x), and then evaluate "x" to 0, so, calculating we have:

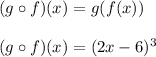
$(g\circ f)(x)=g(f(x))\\\\(g\circ f)(x)=(2x-6)^(3)$

Now that we have the composite function, we need to evaluate "x" equal to 0, so:

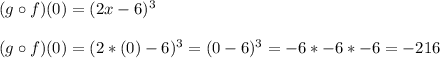
$(g\circ f)(0)=(2x-6)^(3)\\\\(g\circ f)(0)=(2*(0)-6)^(3)=(0-6)^(3)=-6*-6*-6=-216$

Hence, we have that:

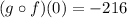
$(g\circ f)(0)=-216$

Have a nice day!