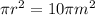Question

A cylinder has a volume of 140pi

cubic meters and a height of 14 meters. What is the area of the base?

Answer 1

The area of the base is
`10\pi m^2`

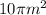
Explanation:

The volume of a cylinder is calculated using the formula:

`Volume=\pi r^2h`

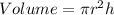
The volume is given to be:

`V=140\pi m^3`

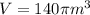
The height of the cylinder is h=14 meters.

We substitute these values into the formula to obtain;

`140\pi=\pi r^2* 14`

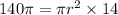
Divide both sides by 14.

`(140\pi)/(14)=\pi r^2`

`10\pi=\pi r^2`

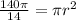
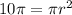
The area of the base is a circle which is
`\pi r^2=10\pi m^2`