Question

How to find the derivative of xy = In (x² + y ² )? please show all workings and simplify!

the answer is supposed to be yx^2+y^3 -2x / 2y - x^3-xy^2

Answer 1

Explanation:

Keep in mind that the derivative of ln(u) = u'/u. Here, our u is x^2 + y^2, so the derivative of that will fit in for u'. Let's do this step by step:

`xy=ln(x^2+y^2)`

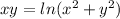
Working on the left first, using the product rule, the derivative (implicite, of course!) is:

`x(dy)/(dx)+1y=ln(x^2+y^2)`

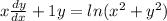
Now we will work on the right side, keeping in mind the rule above for derivatives of natural logs:

`x(dy)/(dx)+1y=(2x+2y(dy)/(dx) )/(x^2+y^2)`

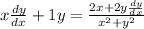
Now we are going to get rid of the donominator on the right by multiplication on both sides:

`(x^2+y^2)(x(dy)/(dx)+1y)=2x+2y(dy)/(dx)`

Distribute on the left to get

`x^3(dy)/(dx)+x^2y+xy^2(dy)/(dx)+y^3=2x+2y(dy)/(dx)`

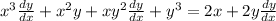
Now collect all the terms with dy/dx in them on one side and everything else goes on the other side:

`x^3(dy)/(dx)+xy^2(dy)/(dx)-2y(dy)/(dx)=2x-x^2y-y^3`

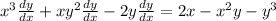
Factor out the common dy/dx:

`(dy)/(dx)(x^3+xy^2-2y)=2x-x^2y-y^3`

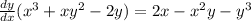
and divide on the left to isolate the dy/dx:

`(dy)/(dx)=(2x-x^2y-y^3)/(x^3+xy^2-2y)`

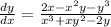
And there you go!