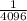Answer:
Explanation:
To solve this we are using the formula for the nth term of a geometric sequence:
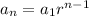
where
 is the first term
is the first term
 is the common ratio
is the common ratio
 is the position of the term in the sequence
is the position of the term in the sequence
The common ratio is just the current term divided by the previous term in the sequence, so
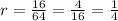 . We can infer from our sequence that its first term is 64, so
. We can infer from our sequence that its first term is 64, so
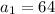 .
.
Replacing values
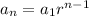

We want to find the 10th term, so the position of the term in the sequence is
 .
.
Replacing values




We can conclude that the 10th term of the sequence is