Question

1. The diagonal of a quadrilateral

is of length 8.5 m and the lengths
of the perpendiculars dropped on
it from the remaining opposite
vertices are 3.5 cm and 4.5 cm.
Find the area of the quadrilateral.​

Answer 1

Consider the length of diagonal is 8.5 cm instead of 8.5 m because length of perpendiculars are in cm.

Given:

Length of the diagonal of a quadrilateral = 8.5 cm

Lengths of the perpendiculars dropped on it from the remaining opposite vertices are 3.5 cm and 4.5 cm.

To find:

The area of the quadrilateral.

Solution:

Diagonal divides the quadrilateral in 2 triangles. If diagonal is the base of both triangles then the lengths of the perpendiculars dropped on it from the remaining opposite vertices are heights of those triangles.

According to the question,

Triangle 1 : Base = 8.5 cm and Height = 3.5 cm

Triangle 2 : Base = 8.5 cm and Height = 4.5 cm

Area of a triangle is

`Area=(1)/(2)* base * height`

Using this formula, we get

`Area(\Delta 1)=(1)/(2)* 8.5* 3.5`

`Area(\Delta 1)=14.875`

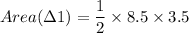
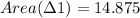
and

`Area(\Delta 2)=(1)/(2)* 8.5* 4.5`

`Area(\Delta 2)=19.125`

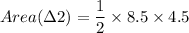
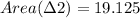
Now, area of the quadrilateral is

`Area=Area(\Delta 1)+Area(\Delta 2)`

`Area=14.875+19.125`

`Area=34`

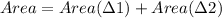
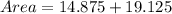
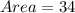
Therefore, the area of the quadrilateral is 34 cm².