Question

How to find the derivative of x + y2 = ln(x/y) ? please show all workings and simplify!

the answer is supposed to be y^2-x/xy

Answer 1

Explanation:

If your function is

`x+y^2=ln((x)/(y) )`, that is definitely not the answer you should get after taking the derivative implicitely. Rewrite your function to simplify a bit:

`x+y^2=ln(x)-ln(y)`

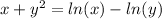
Take the derivative of x terms like "normal", but taking the derivative of y with respect to x has to be offset by dy/dx. Doing that gives you:

`1+2y(dy)/(dx)=(1)/(x)-(1)/(y)(dy)/(dx)`

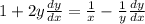
Collect the terms with dy/dx on one side and everything else on the other side:

`2y(dy)/(dx)+(1)/(y)(dy)/(dx)=(1)/(x)-1`

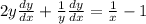
Now factor out the common dy/dx term, leaving this:

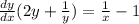`(dy)/(dx)(2y+(1)/(y))=(1)/(x)-1`Now divide on the left to get dy/dx alone:

`(dy)/(dx)=((1)/(x)-1 )/(2y+(1)/(y) )`

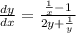
Simplify each set of fractions to get:

`(dy)/(dx)=((1-x)/(x) )/((2y^2+1)/(y) )`

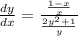
Bring the lower fraction up next to the top one and flip it upside down to multiply:

`(dy)/(dx)=(1-x)/(x)`×
`(y)/(2y^2+1)`

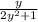
Simplifying that gives you the final result:

`(dy)/(dx)=(y-xy)/(x(2y^2+1))`

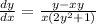
or you could multiply in the x on the bottom, as well. Same difference as far as the solution goes. You'd use this formula to find the slope of a function at a point by subbing in both the x and the y coordinates so it doesn't matter if you do the distribution at the very end or not. You'll still get the same value for the slope.