Answer:
The larger model’s volume is 3 times greater than the volume of the smaller model
Explanation:
we know that
The volume of a pyramid is equal to

where
B is the area of the base of pyramid
h is the height of the pyramid
Find the volume of the smaller model
we have

substitute

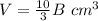
Find the volume of the larger model
we have
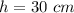
substitute
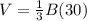
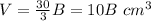
To find how many times greater than the smaller model is the larger model’s volume, divide the volume of the larger model by the volume of the smaller model
so
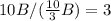
The larger model’s volume is 3 times greater than the volume of the smaller model