Question

What is the energy of a photon that has the same wavelength as an electron having a kinetic energy of 15 ev?

Answer 1

Answer:
`6.268(10)^(-16)J`

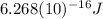
Step-by-step explanation:

The kinetic energy of an electron
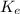`K_(e)` is given by the following equation:

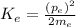`K_(e)=((p_(e))^(2) )/(2m_(e))` (1)

Where:

`K_(e)=15eV=2.403^(-18)J=2.403^(-18)(kgm^(2))/(s^(2))`

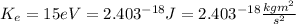
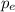`p_(e)` is the momentum of the electron

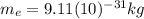`m_(e)=9.11(10)^(-31)kg` is the mass of the electron

From (1) we can find
`p_(e)`:

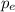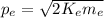`p_(e)=\sqrt{2K_(e)m_(e)}` (2)

`p_(e)=\sqrt{2(2.403^(-18)J)(9.11(10)^(-31)kg)}`

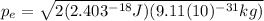
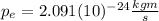`p_(e)=2.091(10)^(-24)(kgm)/(s)` (3)

Now, in order to find the wavelength of the electron
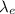`\lambda_(e)` with this given kinetic energy (hence momentum), we will use the De Broglie wavelength equation:

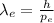`\lambda_(e)=(h)/(p_(e))` (4)

Where:

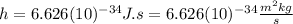`h=6.626(10)^(-34)J.s=6.626(10)^(-34)(m^(2)kg)/(s)` is the Planck constant

So, we will use the value of
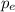`p_(e)` found in (3) for equation (4):

`\lambda_(e)=(6.626(10)^(-34)J.s)/(2.091(10)^(-24)(kgm)/(s))`

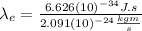
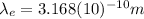`\lambda_(e)=3.168(10)^(-10)m` (5)

We are told the wavelength of the photon
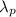`\lambda_(p)` is the same as the wavelength of the electron:

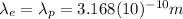`\lambda_(e)=\lambda_(p)=3.168(10)^(-10)m` (6)

Therefore we will use this wavelength to find the energy of the photon
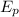`E_(p)` using the following equation:

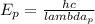`E_(p)=(hc)/(lambda_(p))` (7)

Where
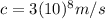`c=3(10)^(8)m/s` is the spped of light in vacuum

`E_(p)=((6.626(10)^(-34)J.s)(3(10)^(8)m/s))/(3.168(10)^(-10)m)`

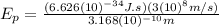
Finally:

`E_(p)=6.268(10)^(-16)J`