Question

105. Suppose that the probability that an adult in America will watch the Super Bowl is 40%. Each person is considered independent. We are interested in the number of adults in America we must survey until we find one who will watch the Super Bowl. a. In words, define the random variable X. b. List the values that X may take on. c. Give the distribution of X. X ~ _____(_____,_____) d. How many adults in America do you expect to survey until you find one who will watch the Super Bowl? e. Find the probability that you must ask seven people. f. Find the probability that you must ask three or four people.

Answer 1

a. X is the number of adults in America that need to be surveyed until finding the first one that will watch the Super Bowl.

b. X can take any integer that is greater than or equal to 1.
`\rm X\in \mathbb{Z}^(+)`.

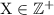c.
`\rm X \sim NB(1, 0.40)`.

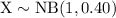d.
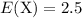`E(\rm X) = 2.5`.

e.
`P(\rm X = 7) = 0.0187`.

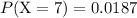f.
`P(\text{X} = 3) +P(\text{X} = 4) = 0.230`.

Explanation:

a.

In this setting, finding an adult in America that will watch the Super Bowl is a success. The question assumes that the chance of success is constant for each trial. The question is interested in the number of trials before the first success. Let X be the number of adults in America that needs to be surveyed until finding the first one who will watch the Super Bowl.

b.

It takes at least one trial to find the first success. However, there's rare opportunity that it might take infinitely many trials. Thus, X may take any integer value that is greater than or equal to one. In other words, X can be any positive integer:
`\rm X\in \mathbb{Z}^(+)`.

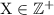c.

There are two discrete distributions that may model X:

• The geometric distribution. A geometric random variable measures the number of trials before the first success. This distribution takes only one parameter: the chance of success on each trial.
• The negative binomial distribution. A negative binomial random variable measures the number of trials before the r-th success. This distribution takes two parameters: the number of successes
  `r` and the chance of success on each trial
  `p`.

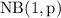`\rm NB(1, p)` (note that
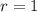`r=1`) is equivalent to
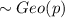`\sim Geo(p)`. However, in this question the distribution of
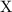`\rm X` takes two parameters, which implies that
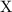`\rm X` shall follow the negative binomial distribution rather than the geometric distribution. The probability of success on each trial is
`40\% = 0.40`.

`\rm X\sim NB(1, 0.40)`.

d.

The expected value of a negative binomial random variable is equal to the number of required successes over the chance of success on each trial. In other words,

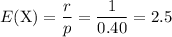`\displaystyle E(\text{X}) = (r)/(p) = (1)/(0.40) = 2.5`.

e.

`P(\rm X = 7) = 0.0187`.

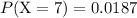Some calculators do not come with support for the negative binomial distribution. There's a walkaround for that as long as the calculator supports the binomial distribution. The r-th success occurs on the n-th trial translates to (r-1) successes on the first (n-1) trials, plus another success on the n-th trial. Find the chance of (r-1) successes in the first (n-1) trials and multiply that with the chance of success on the n-th trial.

f.

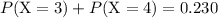`P(\text{X} = 3)+P(\text{X} = 4) = 0.230`.