Given:
Score in first round = 5 points
Score in second, third and fourth rounds was identical.
A participant has to score a total of at least 30 points in the first four rounds combined to move on to the fifth and final round.
To find:
The inequality for the given problem.
Solution:
Let p be the number of points, p, that Steward scored in each of the second, third, and fourth rounds.
Score in first 4 rounds = Score of 1st round + Score of 2nd round + Score of 1s 3rd round + Score of 4th round
Score in first 4 rounds
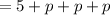
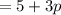
A participant has to score a total of at least 30 points in the first four rounds combined to move on to the fifth and final round. It means the total score in first 4 rounds must be greater than or equal to 30.
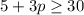
Therefore, the correct option is A.