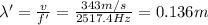Question

The siren on an ambulance is emitting a sound whose frequency is 2250 Hz. The speed of sound is 343 m/s. (a) If the ambulance is stationary and you (the "observer") are sitting in a parked car, what are the wavelength and the frequency of the sound you hear? (b) Suppose that the ambulance is moving toward you at a speed of 26.6 m/s. Determine the wavelength and the frequency of the sound you hear. (c) If the ambulance is moving toward you at a speed of 26.6 m/s and you are moving toward it at a speed of 11.0 m/s, find the wavelength and frequency of the sound you hear.

Answer 1

(a) 2250 Hz, 0.152 m

In this situation, both the ambulance and observer are stationary.

This means that there is no shift in frequency/wavelength due to the Doppler effect. So, the frequency heard by the observer is exactly identical to the frequency emitted by the ambulance:

f = 2250 Hz

While the wavelength is given by the formula:

`\lambda=(v)/(f)`

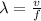
where

v = 343 m/s is the speed of sound

f = 2250 Hz is the frequency of the sound

Substituting, we find

`\lambda=(343 m/s)/(2250 Hz)=0.152 m`

(b) 2439.2 Hz, 0.141 m

The Doppler effect formula for a moving source is

`f'=((v)/(v+v_s))f`

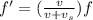
where

f' is the apparent frequency

f is the original frequency

v is the speed of sound

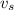`v_s` is the velocity of the source (the ambulance), which is positive if the source is moving away from the observer, negative otherwise

Here the ambulance is moving toward the observer, so

`v_s = -26.6 m/s`

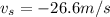
Substituting into the formula, we find the frequency heard by the observer:

`f'=((343 m/s)/(343 m/s-26.6 m/s))(2250 Hz)=2439.2 Hz`

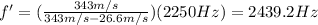
while the wavelength seen by the observer will be:

`\lambda' = (v)/(f')=(343 m/s)/(2439.2 Hz)=0.141 m`

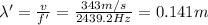
(c) 2517.4 Hz, 0.136 m

In this situation, we must use the most general formula for the Doppler effect, which is

`f'=((v+v_r)/(v+v_s))f`

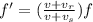
where

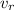`v_r` is the velocity of the observer, which is positive if the observer is moving toward the source, negative otherwise

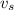`v_s` is the velocity of the source (the ambulance), which is positive if the source is moving away from the observer, negative otherwise

In this situation,

`v_s = -26.6 m/s`

`v_r = +11.0 m/s`

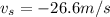
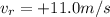
Therefore, the frequency heard by the observer is

`f'=((343 m/s+11.0 m/s)/(343 m/s-26.6 m/s))(2250 Hz)=2517.4 Hz`

while the wavelength seen by the observer will be:

`\lambda' = (v)/(f')=(343 m/s)/(2517.4 Hz)=0.136 m`