This triangle is not a right triangle. How do we solve this then? You will use the law of sine with is shown below:

What we know is shown in the image attached below:
Plug what you know into the law of sine
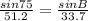
To solve for sinB cross multiply
sin75*33.7 = sinB * 51.2
32.55 = sinB*51.2
Divide 51.2 to both sides to isolate sinB
32.55 / 51.2 = sinB / 51.2
0.63577 = sinB
To find B you must use arcsin:
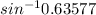
39.477
^^^This is your rough estimate but you can simply keep it to 39 degrees
This means that your answer is correct!
Hope this helped!