Question

Please help me with this word problem!

Answer 1

`f(g)=25g`

Explanation:

Let
`g` be the number of gallons so
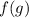`f(g)` is the number of miles traveled per
`g` gallons.

We know for our problem that Brian's car gets 25 miles per gallon. Since the gallons is represented by
`g`, his car will travel a total distance of 25g (where g is the number of gallons.

We also know that the total distance is given by
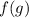`f(g)`, so we can put the two expressions together to get our function:

`f(g)=25g`

Let's check:

- If he uses 1 gallon (g=1), so

`f(1)=25(1)`

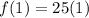
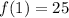`f(1)=25` miles

He will travel 25 miles with one gallon.

- If he uses 2 gallons (g=2), so

`f(2)=25(2)`

`f(2)=50`

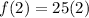
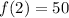
He will travel 50 miles with two gallon.