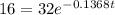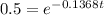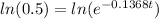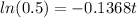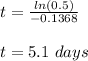Question

A 32 gram sample of a substance that’s a by-product of fireworks has a k-value of 0.1368. Find the substance’s half-life, in days. Use formula

N=N0e-kt, t= time in days.
HELP PLS

Answer 1

5.1

PLATO answer

Explanation:

Answer 2

t=5.1 days

Explanation:

We know that the formula is:

`N = N_0e^(-kt)`

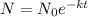
Where N is the amount of substance after a time t,
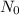`N_0` is the initial amount of substance, k is the rate of decrease, t is the time in days.

`k=0.1368\\N_0 =32`

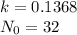
We want to find the average life of the substance in days

The half-life of the substance is the time it takes for half the substance to disintegrate.

Then we equal N to 16 gr and solve the equation for t

`16= 32e^(-0.1368t)`

`0.5= e^(-0.1368t)`

`ln(0.5)= ln(e^(-0.1368t))`

`ln(0.5)= -0.1368t`

`t= (ln(0.5))/(-0.1368)\\\\t=5.1\ days`