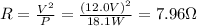Answer:
Step-by-step explanation:
First of all, we can calculate the power dissipated by the resistor. We have:
E = 181 J is the energy produced
t = 9.99 s is the time interval
So, the power dissipated is
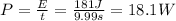
But the power dissipated can also be written as
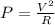
where
V = 12.0 V is the potential difference across the resistor
R is the resistance
Solving for R, we find