(a) 4.0 s
The acceleration of the car is given by
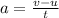
where
v is the final velocity
u is the initial velocity
t is the time interval
For this car, we have
v = 0 (the final speed is zero since the car comes to a stop)
u = 20 m/s is the initial velocity
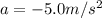 is the deceleration of the car
is the deceleration of the car
Solving the equation for t, we find the time needed to stop the car:
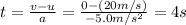
(b) 40 m
The stopping distance of the car can be calculated by using the equation
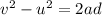
where
v = 0 is the final velocity
u = 20 m/s is the initial velocity
a = -5.0 m/s^2 is the acceleration of the car
d is the stopping distance
Solving the equation for d, we find
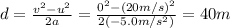
(c)
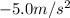
The deceleration is given by the problem, and its value is
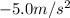 .
.
(d) 5000 N
The net force applied on the car is given by
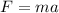
where
m is the mass of the car
a is the magnitude of the acceleration
For this car, we have
m = 1000 kg is the mass
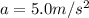 is the magnitude of the acceleration
is the magnitude of the acceleration
Solving the formula, we find
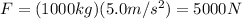
(e)
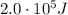
The work done by the force applied by the car is
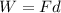
where
F is the force applied
d is the total distance covered
Here we have
F = 5000 N
d = 40 m (stopping distance)
So, the work done is
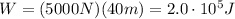
(f) The kinetic energy is converted into thermal energy
Step-by-step explanation:
when the breaks are applied, the wheels stop rotating. The car slows down, as a result of the frictional forces between the brakes and the tires and between the tires and the road. Due to the presence of these frictional forces, the kinetic energy is converted into thermal energy/heat, until the kinetic energy of the car becomes zero (this occurs when the car comes to a stop, when v = 0).