Answer:
The sum of all the terms in series is 875.
Explanation:
Given : If the first term of the series is 30 and the 14th term is 95,
To find : What is the sum of all the terms of the series?
Solution :
The first term of the series is 30 i.e. a=30
The 14th term of series is 95 i.e.
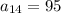
We know that in arithmetic series the 14th term is defined as
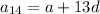
Substitute the value of a,
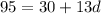
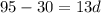
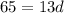
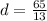
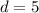
The common difference is 5.
The sum of the series is given by,
![S_(n)=(n)/(2)[2a+(n-1)d]](https://img.qammunity.org/2020/formulas/mathematics/high-school/18ly1pcix4xprbsf3lks1jjup3948pknar.png)
![S_(14)=(14)/(2)[2(30)+(14-1)5]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/glswctji4tcqsvoh1oxeravx9ahzugw65n.png)
![S_(14)=7[60+(13)5]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/y2a6r4rfuhom95e1b1i23usrsj20kfwncb.png)
![S_(14)=7[60+65]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/2vw2babwpg3237uzif1p80mwcxu0oug7g5.png)
![S_(14)=7[125]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/674tcnmx0tp62iaqoebq88wug6cj846yu1.png)
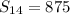
Therefore, The sum of all the terms in series is 875.