QUESTION 11
Given :
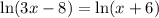
We take antilogarithm of both sides to get:
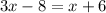
Group similar terms to get:
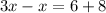
Simplify both sides to get:
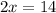
Divide both sides by 2 to obtain:
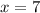
12. Given;
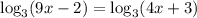
We take antilogarithm to obtain:

Group similar terms to get:
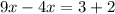
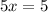
We divide both sides by 5 to get:

13.
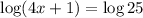
We take antilogarithm to get:
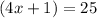
Group similar terms
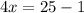
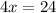
Divide both sides by 4

14. Given ;
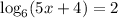
We take antilogarithm to get:
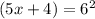
Simplify:

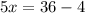

Divide both sides by 5
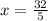
Or
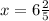
15. Given:
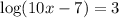
We rewrite in the exponential form to get:
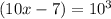

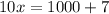
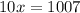
Divide both sides by 10
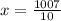
16. Given:
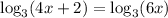
We take antilogarithm to obtain:
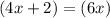
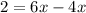
Simplify

Divide both sides by 2

17. Given
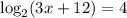 .
.
We rewrite in exponential form:
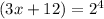
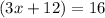
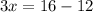
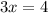
Divide both sides by 3
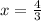
18. Given
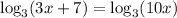
We take antilogarithm to get:
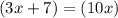
Group similar terms:
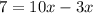
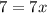
We divide both sides by 7

19. Given:
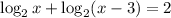
Apply the product rule to simplify the left hand side
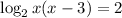
We take antilogarithm to obtain:
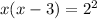
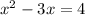
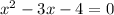
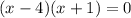
x=-1 or x=4
But x>0, therefore x=4
20. Given
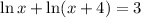
Apply product rule to the LHS
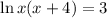
Rewrite in the exponential form to get:
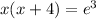
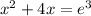
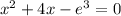
This implies that:
 or
or
