Question

A runner is moving at a constant speed of 8.00 m/s around a circular track. If the distance from the runner to the center of the track is 28.2 m, what is the centripetal acceleration of the runner?

1.13 m/s2
0.284 m/s2
3.53 m/s2
2.27 m/s2

Answer 1

Answer: Last option

2.27 m/s2

Step-by-step explanation:

As the runner is running at a constant speed then the only acceleration present in the movement is the centripetal acceleration.

If we call a_c to the centripetal acceleration then, by definition

`a_c =w^2r = (v^2)/(r)`

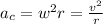
in this case we know the speed of the runner

`v =8.00\ m/s`

The radius "r" will be the distance from the runner to the center of the track

`r = 28.2\ m`

`a_c = (8^2)/(28.2)\ m/s^2`

`a_c = 2.27\ m/s^2`

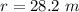
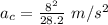
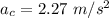
The answer is the last option