Answer:
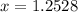
Explanation:
Assuming the equation to solve is
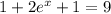
We can first simplify as:

to solve an equation with e and x as an exponent, we need to take "natural log (ln)" on both sides and also use the property:
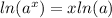
And also remember that ln e = 1
Now we have:
